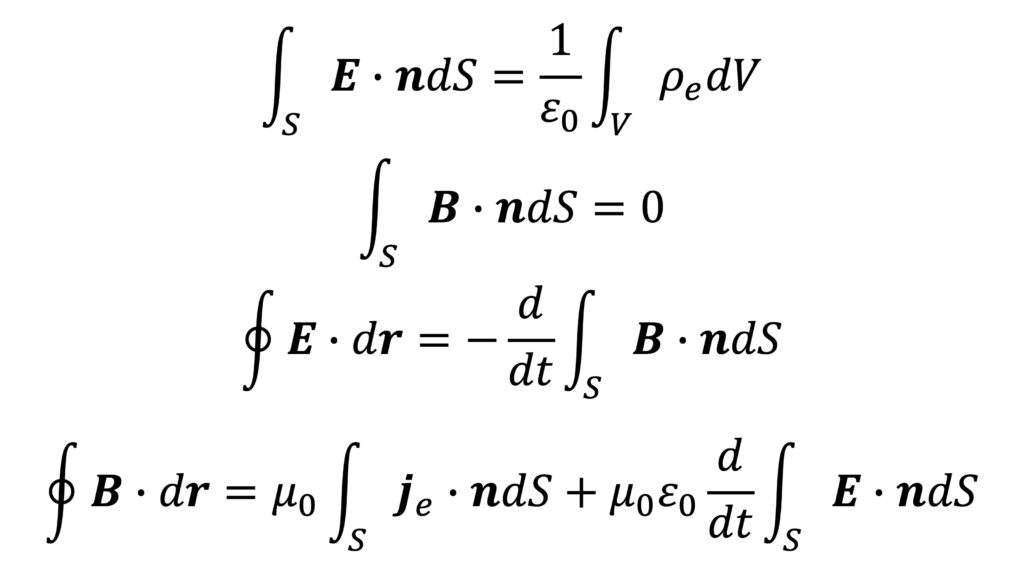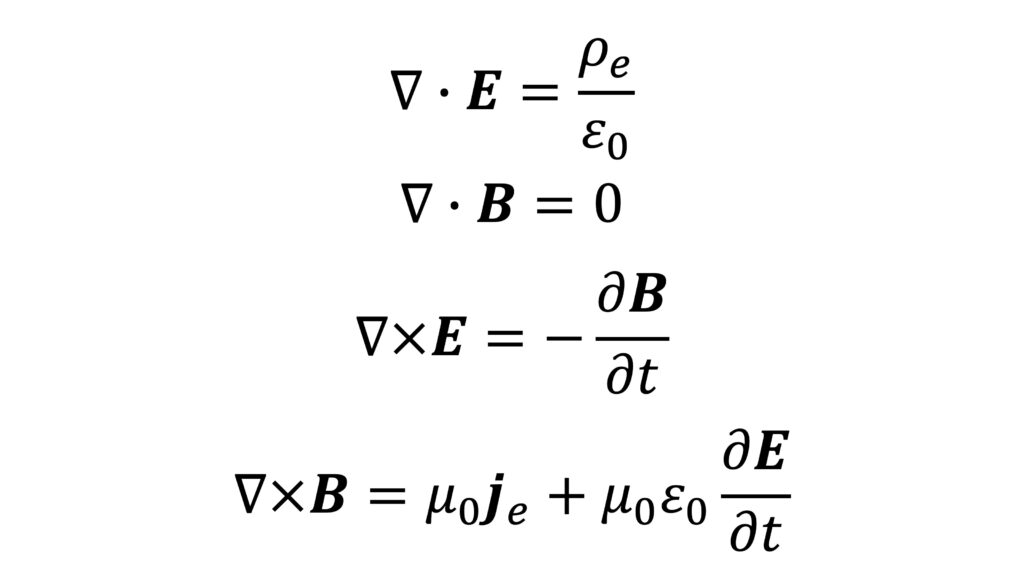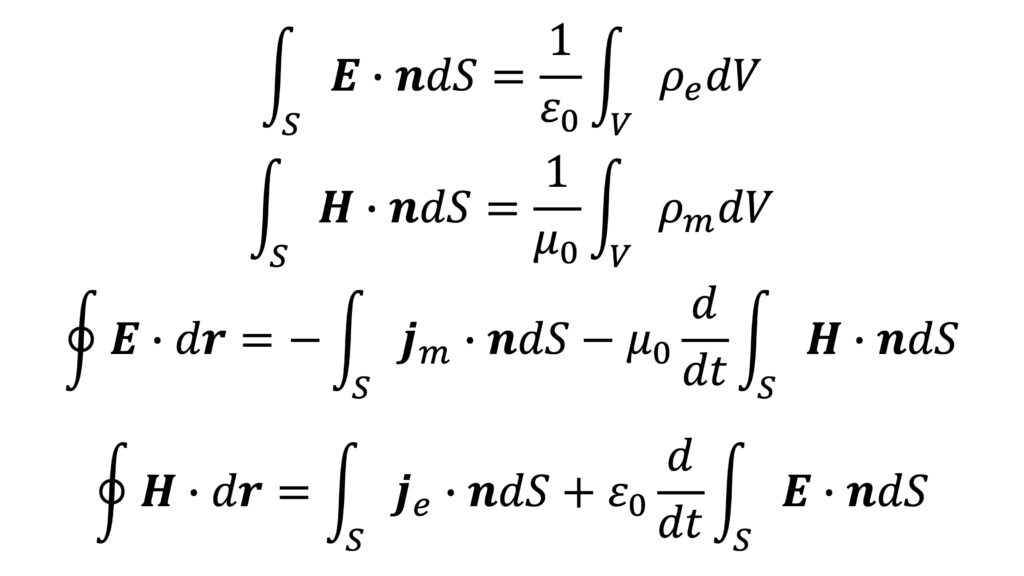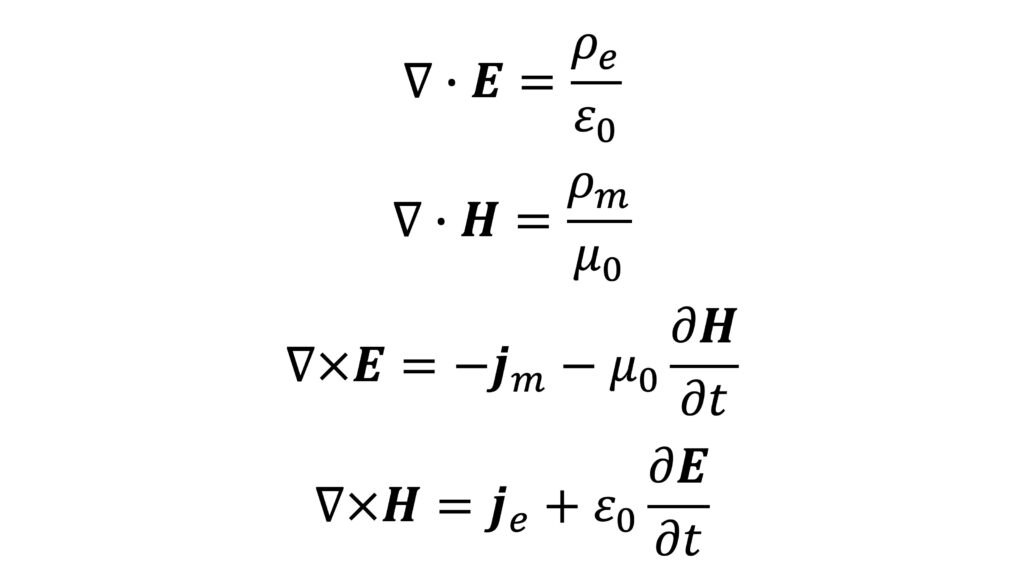§1:場の概念
この章では, 物理的直感に即した近接作用の考え方から, 場の概念を導入する.
- 近接作用と遠隔作用
- 電磁場の導入
- ローレンツ力〜磁場は仕事をしない〜
§2:電磁気学の表現論
この章では, 電磁気学を記述する上で必要不可欠なベクトル解析について取り扱う.
- グラディエント(勾配)
- ダイバージェンス(発散)
- ローテーション(回転)
- ガウスの定理(面積分⇔体積分)
- ストークスの定理(線積分⇔面積分)
§3:マクスウェル方程式
この章では, 電荷と磁荷を仮定して, E-H対応のマクスウェル方程式の対称性を確認した後, 現実に即してE-B対応のマクスウェル方程式に書き換えることで, 磁場と磁束密度の違いを正しく認識してもらうことを目標にする.
- E-H対応とE-B対応
- E-H対応のマクスウェル方程式(積分形)
- E-H対応のマクスウェル方程式(微分形)
- E-B対応のマクスウェル方程式(積分形)
- E-B対応のマクスウェル方程式(微分形)
§4:電磁気現象の各論
この章では, マクスウェル方程式を様々な系に適用することで, 高校物理で学ぶ各論を全て"導出"できることを示していく. このことから, 原理的には電磁気現象は全てマクスウェル方程式で記述できることが実感されるだろう.
- クーロンの法則
- ビオ・サバールの法則
- アンペールの法則
Appendix:波の表現論
- 波動方程式
- 波長と波数
- 振動数と角速度
- 位相速度と群速度
- 平面波と球面波