- マクスウェル方程式の各論を解説し、帰納的にマクスウェル方程式を導出する方法
- マクスウェル方程式で表現された4つの法則を原理として認め、そこから各論を演繹的に展開していく方法
帰納的に電磁気学を組み立てる
現在、多くの高等学校や大学の授業が採用する立場。
各式にあたる内容を個別に扱ったあと、最後にマクスウェル方程式を示して終わることが多い。
ただし、この方法ではマクスウェル方程式の取り扱いが小さくなり, その式が電磁気の現象を見事に記述できているというのを実感できていないケースが散見される。
演繹的に電磁気学を組み立てる
マクスウェル方程式で表現された4つの法則を原理として認める立場。
これは電磁気学現象を個別に見る際に俯瞰的な立場から理解することができる一方で, 整理された体系なので、物理が実証科学であるという側面が少し薄れてしまうことは否めない。
マクスウェル方程式(積分系)
$$\int_S \bf{E}\cdot\bf{n}~\it{dS}=\frac{1}{\epsilon_0}\int_V \rho~dV\tag{1}$$
$$\oint_C \bf{E}\cdot\it{d}\bf{r}\rm=-\it\frac{d}{dt}\int_S \bf{B}\cdot\bf{n}~\it{dS}\tag{2}$$
$$\int_S \bf{B}\cdot\bf{n}~\it{dS}=\rm0\tag{3}$$
$$c^{2}\oint_C \bf{B}\cdot\it{d}\bf{r}\rm=\it\frac{1}{\epsilon_0}\int_S \bf{j}\cdot\bf{n}~\it{dS}+\frac{d}{dt}\int_S \bf{E}\cdot\bf{n}~\it{dS}\tag{4}$$
マクスウェル方程式(微分系)
$$\nabla\cdot\bf{E}\it=\frac{\rho}{\epsilon_0}\tag{1}$$
$$\nabla\times\bf{E}\it=-\frac{\partial\bf{B}}{\partial\it{t}}\tag{2}$$
$$\nabla\cdot\bf{B}\it=\rm0\tag{3}$$
$$c^{2}\nabla\times\bf{B}\it=\frac{\bf{j}}{\epsilon_0}\it+\frac{\partial\bf{E}}{\partial\it{t}}\tag{4}$$

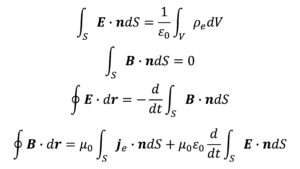
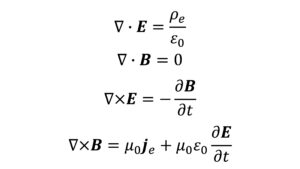
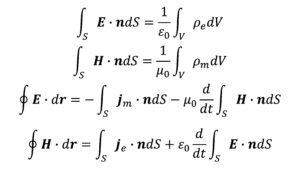
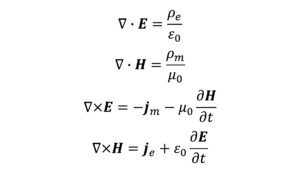
コメント