ここでは電磁場が従う4つの方程式「マクスウェル方程式」の積分系/微分形表示をまず示し、その変換の途中計算や各式の内容を解説していく。
目次
マクスウェル方程式(積分系)
$$\int_S \bf{E}\cdot\bf{n}~\it{dS}=\frac{1}{\epsilon_0}\int_V \rho~dV\tag{1}$$
$$\oint_C \bf{E}\cdot\it{d}\bf{r}\rm=-\it\frac{d}{dt}\int_S \bf{B}\cdot\bf{n}~\it{dS}\tag{2}$$
$$\int_S \bf{B}\cdot\bf{n}~\it{dS}=\rm0\tag{3}$$
$$c^{2}\oint_C \bf{B}\cdot\it{d}\bf{r}\rm=\it\frac{1}{\epsilon_0}\int_S \bf{j}\cdot\bf{n}~\it{dS}+\frac{d}{dt}\int_S \bf{E}\cdot\bf{n}~\it{dS}\tag{4}$$
マクスウェル方程式(微分系)
$$\nabla\cdot\bf{E}\it=\frac{\rho}{\epsilon_0}\tag{1}$$
$$\nabla\times\bf{E}\it=-\frac{\partial\bf{B}}{\partial\it{t}}\tag{2}$$
$$\nabla\cdot\bf{B}\it=\rm0\tag{3}$$
$$c^{2}\nabla\times\bf{B}\it=\frac{\bf{j}}{\epsilon_0}\it+\frac{\partial\bf{E}}{\partial\it{t}}\tag{4}$$

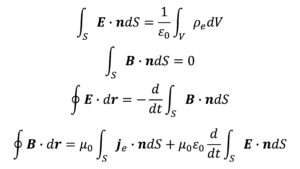
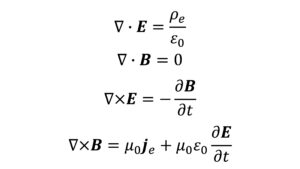
コメント